De SPSS begeleider waar je wél wat aan hebt
Wij staan voor je klaar staat zijn wanneer jij dat nodig hebt, luisteren naar je en nemen jouw vragen serieus (naast dat we die natuurlijk ook gaan beantwoorden)
Z-score, wat is het?
Een Z-score geeft aan hoeveel standaarddeviaties een observatie van het gemiddelde af zit. Je krijgt dus je plek ten opzichte van het gemiddelde, uitgedrukt in een standaard maat. Dit heeft als voordeel dat je direct kunt zien hoe goed iemand scoort ten opzichte van de rest.
Hieronder lees je uitleg over de z-score. Mocht je daar niet uitkomen staan wij voor je klaar om ervoor te zorgen dat jij de z-scores gaat begrijpen. Neem in dat geval contact met ons op door het contactformulier in te vullen!
Z-score, de formule
De formule van de Z-score bestaat uit een observatie Xi, het gemiddelde uit de populatie (ook wel de verwachtingswaarde genoemd) μ, en de standaarddeviatie van de populatie σ.
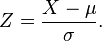
Als de verwachtingswaarde en de standaarddeviatie in de populatie onbekend zijn, kunnen deze ook geschat worden dmv een steekproef.
Z-score, een voorbeeld
Om het helemaal duidelijk te krijgen, hebben we het volgende voorbeeld: Stel je gaat met 4 andere vrienden een avondje de kroeg in en jullie betalen ieder €50 aan de bierpot. De standaarddeviatie is het briefje van €10. Net voordat je het eerste drankje wil bestellen, komt er nog een 6e vriend bij. Hij heeft echter maar €35 meegenomen en wil dat in de bierpot stoppen. Wat is dan zijn Z-score? Het invullen van de formule geeft dan: Z-score = (35-50)/10 = -1,5. Een Z-score van -1,5 betekent dus dat deze persoon anderhalf briefje van €10 onder het gemiddelde zit.
In SPSS kan je onder het menu “:analyze –> descriptive statistics –> descriptives” een vakje vinden dat je moet aanvinken genaamd “save as standardized values as variables”. Je krijgt dan Z-scores van je variabele als nieuwe variabele achterin je dataset. Zie afbeelding hieronder:

Salary is in euro’s per dag, ZSalary is in gestandaardiseerde Z-scores
Waarom is zo’n gestandaardiseerde (z-)score zo belangrijk?
Als eerste kan je aan het teken (positief of negatief) meteen zien wie er van de steekproef boven en wie onder het gemiddelde zitten.Ook is het mogelijk om scores op verschillende variabelen met elkaar te vergelijken, omdat de meeteenheid van een variabele er op deze manier niet meer toe doet. Je kan Z-scores van verschillende variabelen dus vergelijken met elkaar en dan direct zien op welke je het hoogst scoort.Maar daarnaast wordt de Z-verdeling ook wel de normale verdeling genoemd. Z-scores kun je namelijk makkelijk vertalen in oppervlaktes onder de normaal curve, en dus omzetten in kansen of percentages. Er is namelijk een vuistregel (de empirische regel) die zegt dat 68% van de personen tussen een Z-score van -1 en 1 zit, dat 95% van de personen een Z-score tussen -2 en 2 heeft, en 99,7% binnen 3 standaarddeviaties ten opzichte van het gemiddelde zit.
Wat zijn outliers?
Personen (of beter gezegd: cases/metingen/data-punten) met een Z-score groter dan 3 of kleiner dan -3 kun je dus vaak beschouwen als outliers. Deze personen zitten dus in de uiterste 5% van de scores. Via de ‘Descriptive Statistics’> ‘Explore’ kunnen door middel van de options knop outliers opgevraagd worden. Hierdoor zal in de output een boxplot weergegeven worden met eventuele outliers aangegeven met cirkels en sterretjes. Een andere mogelijkheid is om via de ‘Descriptive Statistics’> ‘Descriptives’ gebruik te maken van de functie ‘Save standardized values’om de z-scores op te slaan in de dataset. Vervolgens kan je in de dataset de outliers met een z-score groter dan 3 of kleiner dan -3 verwijderd worden.
Onze methode in één minuut
Sanne (student) over onze scriptiebegeleiding
Meer weten, check dan onze:
SPSS nog net geen chinees voor je?
De weg kwijt in SPSS? Is het kiezen van de juiste toets als het praten in Chinees?? Geen nood, wij helpen je om de controle terug te krijgen!
Nodige bevestiging in je keuzes
Het werken met SPSS betekent veel keuzes en fouten maken. Wij kijken met je mee en bespreken wat je hebt gedaan zodat jij je er weer zeker over voelt
Deadline toch halen (realistische planning)
Een naderende deadline icm SPSS zorgt voor stress. We stellen samen een realistische planning op zodat jij die deadline gaat halen!
Vertel ons wie je bent en we gaan samen met je aan de slag!
Nog één stap en je hebt je gratis kennismaking geregeld 🙂
Waarom Afstudeerbegeleider?
- begrijpen wat je aan het doen bent
- eindelijk weer stappen voorwaarts gaan maken
- die deadline halen
- begeleiders die proactief meedenken
- die beschikbaar zijn wanneer jij het nodig hebt
- naar je luisteren

Wat zeggen andere studenten over onze begeleiding



