De SPSS begeleider waar je wél wat aan hebt
Wij staan voor je klaar staat zijn wanneer jij dat nodig hebt, luisteren naar je en nemen jouw vragen serieus (naast dat we die natuurlijk ook gaan beantwoorden)
Hypothese one sample t-test
De one sample t-test kent de volgende hypothesen:
H0 (nul hypothese):
Het gemiddelde cijfer van deze klas is gelijk aan 6 (landelijk gemiddelde).
HA (alternatieve hypothese)
Het gemiddelde cijfer van deze klas is ONGELIJK 6 (landelijk gemiddelde).
We geven dus geen richting aan. Een voorbeeld van richting aangeven is: “het gemiddelde van de klas is hoger dan 6”. Als we geen richting aangeven zeggen we: “het gemiddelde in ongelijk aan 6”. Dan kan het gemiddelde dus hoger of lager zijn dan 6. Aangezien onze hypothese geen richting bevat (zie boven) toetsen we tweezijdig. We willen met 95% (standaard) zekerheid kunnen zeggen dat we de nul hypothese moeten verwerpen en de alternatieve hypothese aannemen.
Output tabellen van de one sample t-test
Stap 1
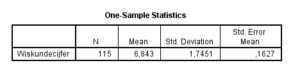
In de eerste tabel in de output van de one sample t-test worden de statistieken van de klas (complete dataset) gegeven. Hier staat simpelweg dat de klas uit 115 personen bestond, een gemiddelde had van 6,84, een SD had van 1,75 en een SE van ,16. Deze kan je later rapporteren bij het beschrijven van je resultaten, maar hoef je voor de test verder niks mee te doen.
De volgende tabel gaat je vertellen of het gemiddelde cijfer van de klas verschilt van 6.
Interpreteren output one sample t-test
Stap 2
Je hebt het gemiddelde van de klas (6,84) vergeleken met het gegeven gemiddelde 6 (staat in de tabel als test value). Het verschil tussen het gevonden gemiddelde en 6 vind je onder mean difference. Je wilt weten of dit verschil significant is. Dat wil zeggen dat we met 95% of meer zekerheid kunnen zeggen dat dit verschil bestaat. Dat is het geval als onder Sig. een waarde staat van ,05 (5% foutkans) of lager. In het voorbeeld staat onder Sig. een waarde van .000 (minder dan ,01% kans op een fout) dus kleiner dan ,05 (5% kans op een fout) dus mogen we zeggen dat er een (significant) verschil is tussen het gemiddelde van de klas en het gegeven gemiddelde.
Stap 3
In stap 2 hebben we bepaald dat er een verschil is tussen het gemiddelde de klas en het (gegeven) landelijk gemiddelde. We hadden 2 hypothesen namelijk de H0 en de HA. We moeten nu één van de twee verwerpen en de andere aannemen.
We waren voldoende overtuigd (met meer dan 95%) om de H0 te verwerpen en de HA aan te nemen omdat er verschil is tussen het gemiddelde van de klas en het (gegeven) landelijk gemiddelde.
Wat als je er niet uitkomt met de one sample t-test?
Kom je er niet uit met de one sample t-test? Check dan onze online spoedbegeleiding of wat we nog meer voor je kunnen betekenen!
Onze methode in één minuut
Sanne (student) over onze scriptiebegeleiding
Meer weten, check dan onze:
SPSS nog net geen chinees voor je?
De weg kwijt in SPSS? Is het kiezen van de juiste toets als het praten in Chinees?? Geen nood, wij helpen je om de controle terug te krijgen!
Nodige bevestiging in je keuzes
Het werken met SPSS betekent veel keuzes en fouten maken. Wij kijken met je mee en bespreken wat je hebt gedaan zodat jij je er weer zeker over voelt
Deadline toch halen (realistische planning)
Een naderende deadline icm SPSS zorgt voor stress. We stellen samen een realistische planning op zodat jij die deadline gaat halen!
Vertel ons wie je bent en we gaan samen met je aan de slag!
Waarom Afstudeerbegeleider?
- begrijpen wat je aan het doen bent
- eindelijk weer stappen voorwaarts gaan maken
- die deadline halen
- begeleiders die proactief meedenken
- die beschikbaar zijn wanneer jij het nodig hebt
- naar je luisteren
Wat zeggen andere studenten over onze begeleiding
